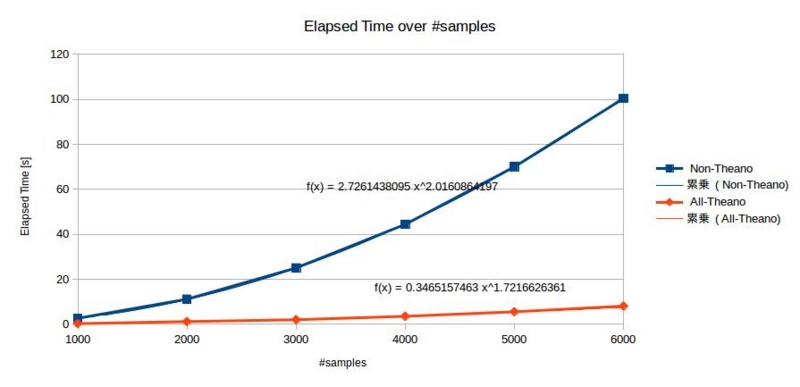
GPU/CPUの計算速度比較
全サンプルの内積計算をNumpy (CPU) vs Theano (GPU)で速度比較をした時のメモ.
実際のサンプルを書く前に,普通に計算する場合を考える.
普通にd-by-nの行列があったら,すべてのサンプルの内積計算の計算量は
で,nに関してsquare-order.
基本的にこういった処理をしたい場合のユースケースとして,あるKernelを使ったGram Matrixの計算や一番簡単な協調フィルタリング(User-by-Item)などが挙げられる.dがスパースの場合は,column2row, row2columnの2重マップを作っておいて計算すると,大体,O(n)になる.
今回は,計算の工夫をしないで愚直に
の計算量の計算をする.
実験設定
タスクはRBF kernelを使ったGram Matrixの計算.
ただし,CPUの場合は上三角行列のみ計算.
rbf_mat_compute_times_over_n.py
#!/usr/bin/env python import numpy as np import theano.tensor as T import time from theano import function from collections import defaultdict d = 100 result = defaultdict(int) for n in np.arange(1000, 7000, 1000): print "#samples = %d" % (n) # dataset X_ = np.random.rand(n, d) gamma_ = 0.01 # Non Theano rbf_mat0 = np.zeros((X_.shape[0], X_.shape[0])) def rbf(x, y, gamma): z = x - y return np.exp(- gamma * z.dot(z)) st0 = time.time() for i, x_ in enumerate(X_): for j, y_ in enumerate(X_): if i <= j: rbf_mat0[i, j] = rbf(x_, y_, gamma_) else: rbf_mat0[i, j] = rbf_mat0[j, i] pass pass et0 = time.time() print "elapsed time (Non-Theano): %f [s]" % (et0 - st0) ## Partial Theano (for-loop) #x = T.dvector("x") #y = T.dvector("y") #gamma = T.dscalar("gamma") #z = (x - y) #rbf_ = T.exp(- gamma * z.dot(z)) #rbf = function([x, y, gamma], rbf_) # #st1 = time.time() #rbf_mat1 = np.zeros((X_.shape[0], X_.shape[0])) #for i, x_ in enumerate(X_): # for j, y_ in enumerate(X_): # rbf_mat1[i, j] = rbf(x_, y_, gamma_) # pass # pass # #et1 = time.time() #print "elapsed time (Partial-Theano): %f [s]" % (et1 - st1) # All theano st2 = time.time() X = T.dmatrix('X') gamma = T.dscalar("gamma") distmat = T.sum( (T.reshape(X, (X.shape[0], 1, X.shape[1])) - X) ** 2, 2) rbf_mat = function([X, gamma], T.exp(- gamma * distmat)) rbf_mat2 = rbf_mat(X_, gamma_) et2 = time.time() print "elapsed time (All-Theano): %f [s]" % (et2 - st2) result[n] = (et0-st0, et2-st2) #print "sanity check" #print rbf_mat0[0, :] #print rbf_mat1[0, :] #print rbf_mat2[0, :]